和对称加密不同,公钥加密(非对称加密)的密钥分为加密密钥(公钥)和解密密钥(私钥)。 公钥是公开的,任何人都有可能知道公钥,并用公钥生成密文,而私钥是保密的,只有解密者才能知道私钥,用它来解密密文获得明文。在这里对使用最广泛的公钥密码算法-- RSA.
RSA 是发明此算法的三位科学家的姓氏的首字母(吐槽一下:外国人的命名真随意)
一. RSA 加密
在RSA中,明文,密钥和密文都是数字, RSA的加密过程可以用如下公式表达:
$$密文 = 明文^E \mod N$$
即: RSA 的密文是明文的 $E$ 次方求模 $N$ 的结果, 或者说,密文是明文的 $E$ 次方除以 $N$ 的余数。这就是整个加密过程,它非常简洁。因此,如果知道了 $E$ 和 $N$ ,那么任何人都可以进行加密运算,也就是说,
$$ E 和 N 是公钥$$
在实际使用中, E 和 N 是经精心计算的数字。
二. RSA 解密
RSA 解密公式如下:
$$ 明文= 密文^D \mod N$$
即,对密文的 $D$ 次方求模 $N$ 运算,就可以得到明文。这里是
$$D 和 N 是私钥 $$
继续阅读
在使用对称加密中,有一些无法避免的问题:
- 密钥如何从加密方传递给解密方。窃听者如果可以劫获密文,那么也可能劫获密钥。
- 如果窃听者破解了密钥,加密方如何将新的密钥安全地交给解密方
1. DH 密钥交换
解决上述问题的一种方法就是 DH 密钥交换 技术 。
DH 密钥交换全称为 Diffie-Hellman 密钥交换 ,是1976年由 Whitfiedl Diffle 和 Martin Hellman 共同发明的一种算法。使用这种方法,通信双方可以在窃听者眼皮子底下来安全地传输密码。
DH 交换的步骤如下:
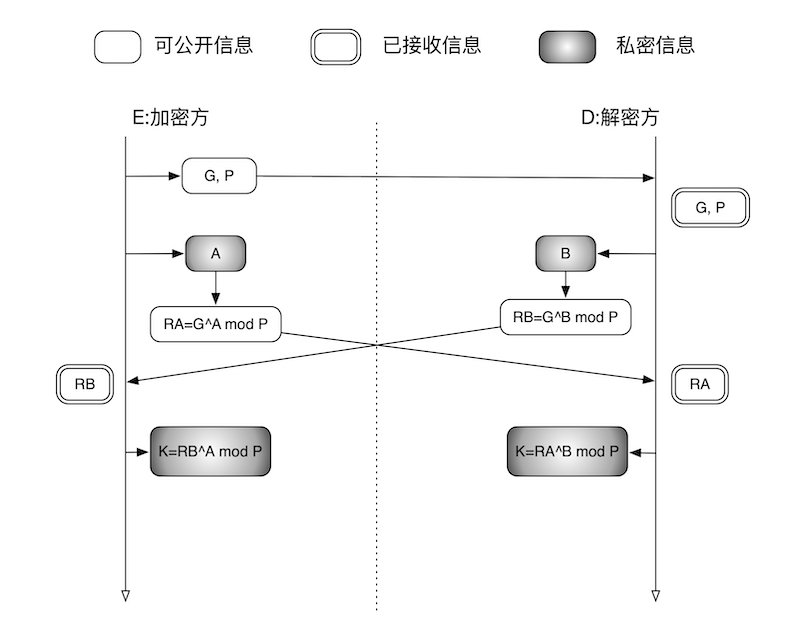
继续阅读
超文本传输安全协议 (HTTPS, Hypertext Transfer Protocol Secure) 常称为HTTP over TLS,HTTP over SSL或HTTP Secure, 是一种使用计算器网络进行安全通信的传输协议。HTTPS经由HTTP进行通信,但利用SSL/TLS来加密数据包。HTTPS开发的主要目的,是提供对网站服务器的身份认证,保护交换数据的隐私与完整性。这个协议由网景公司(Netscape)在1994年首次提出,随后扩展到互联网上。
传输层安全性协议 (TLS, Transport Layer Security) ,及其前身 安全套接层(SSL,Secure Sockets Layer)是一种安全协议,目的是为互联网通信,提供安全及数据完整性保障。网景公司推出HTTPS协议时,以SSL进行加密,这是SSL的起源。IETF将SSL进行标准化,1999年公布第一版TLS标准文件。随后又公布RFC 5246 (2008年8月)与 RFC 6176 (2011年3月)。TLS/SSL 不仅为浏览器提供支持,在邮箱、即时通信、VoIP、网络传真等应用程序中也得到广泛应用。
由此可知,HTTPS 是在 SSL/TLS 之上承载 HTTP 。与HTTP 不同,HTTPS 使用 https:// 做为URL前缀, 默认端口为 443.
为方便,后面将 SSL/TLS 简写为 TLS.
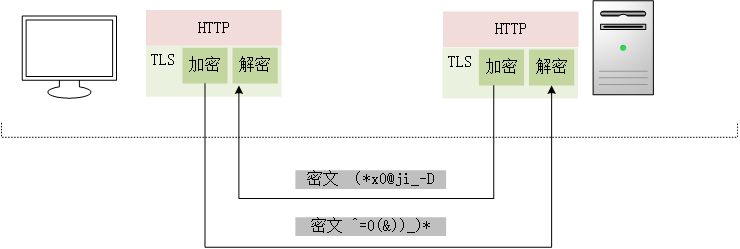
协议的层次
TLS 协议为由 TLS记录协议(TLS record protocol) 与 TLS握手协议(TLS handshake protocol) 这两层协议叠加而成。记录协议负责进行加密,握手协议负责进行加密之外的其它操作。
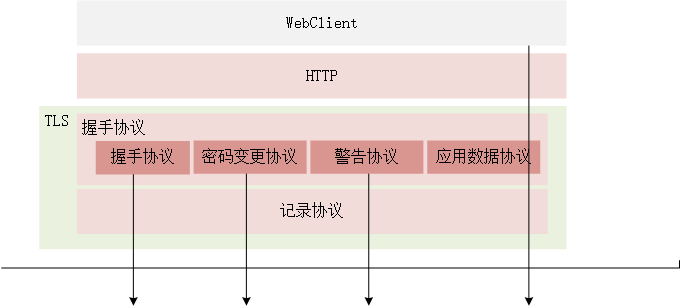
- TLS记录协议 位于握手协议的下层,负责对消息进行加密。它使用了对称加密和消息认证,但具体的算法和共享密钥则是通过握手协议在服务端和客户端之间协商决定的。
- TLS握手协议 分为4个子协议
- 握手协议 负责在客户端与服务端之间协商决定密码算法和共享密钥。基于证书的认证操作也是在这个协议中完成。在握手协商一致后,双方会互发信号来切换密码。
- 密码规格变更协议 负责向通信对象传达密码变更的信号。
- 警告协议 负责在发生错误时将错误信息传递给对方。如果没有发生错误,接下来会使用应用数据协议进行通信。
- 应用数据协议 负责将TLS 上面承载的应用数据传达给通信对象
继续阅读
ECC(Elliptic Curves Cryptography) 属于非对称加密算法的一个重要组成部分。
本文尽量简单地阐述椭圆曲线加密的原理,但需要读者有一些初级的数论与离散数学相关的知识,或者推荐简单地阅读《算法导论》第31章:数论算法。
椭圆曲线
首先需要明确的是,我们讨论的是什么样的曲线。
椭圆曲线有比较复杂的定义: https://en.wikipedia.org/wiki/Elliptic_curve .而我们讨论的椭圆曲线比这个简单,它是以下方程所描述的一条平滑曲线 :
$$y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0$$
它描述的并不是一个椭圆,之所以称它为"椭圆曲线方程", 是因为它源自于求椭圆弧长的椭圆积分的反函数。椭圆曲线是无奇点的,即没有尖点,且不会自相交。当 $a,b$ 的值不同时,椭圆曲线会表现出不同的形态:
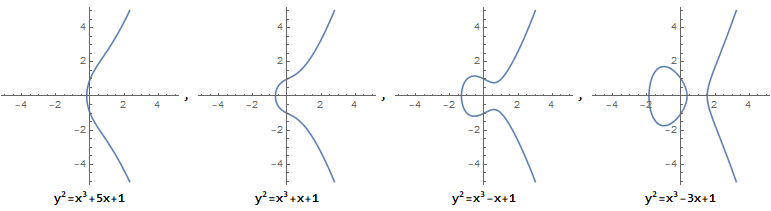
而当 $4a^3 + 27b^2 = 0$ 时, 它不是椭圆曲线:
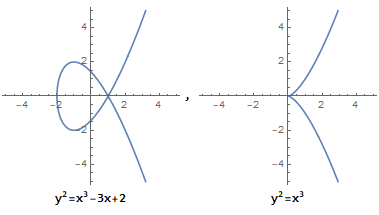
从图中可以看到,椭圆曲线总是 沿 x 轴对称 的。这是因为 $y^2$ 的存在。特殊地,我们规定 无穷远点 也存在于椭圆曲线上。我们用 $0$ 或符号 $O$ 来表示无穷远点,则椭圆曲线在实数域上的定义如下:
$$\{ (x,y) \in \mathbb{R}^2 | y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}$$
继续阅读
SM4分组密码算法,原名SMS4,国家密码管理局于2012年3月21日发布,相关标准为“GM/T 0002-2012《SM4分组密码算法》(原SMS4分组密码算法)”。它是一种分组对称加密算法,分组长度和密钥长度均为 128bit ,加密算法与密码扩展算法均采用 32 轮非线性迭代结构, Sbox 为固定的 8bit 输入 8bit 输出的置换。 数据加/解密的算法结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
SBox
在密码学中,Sbox(Substitution-box,替换盒)是对称密钥加密算法执行替换计算的基本结构。SBox接受一个特定位数的输入,通过查表将其转换为特定位数的输出。SM4 给定的 SBox 如下:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
| 0 |
D6 |
90 |
E9 |
FE |
CC |
E1 |
3D |
B7 |
16 |
B6 |
14 |
C2 |
28 |
FB |
2C |
05 |
| 1 |
2B |
67 |
9A |
76 |
2A |
BE |
04 |
C3 |
AA |
44 |
13 |
26 |
49 |
86 |
06 |
99 |
| 2 |
9C |
42 |
50 |
F4 |
91 |
EF |
98 |
7A |
33 |
54 |
0B |
43 |
ED |
CF |
AC |
62 |
| 3 |
E4 |
B3 |
1C |
A9 |
C9 |
08 |
E8 |
95 |
80 |
DF |
94 |
FA |
75 |
8F |
3F |
A6 |
| 4 |
47 |
07 |
A7 |
FC |
F3 |
73 |
17 |
BA |
83 |
59 |
3C |
19 |
E6 |
85 |
4F |
A8 |
| 5 |
68 |
6B |
81 |
B2 |
71 |
64 |
DA |
8B |
F8 |
EB |
0F |
4B |
70 |
56 |
9D |
35 |
| 6 |
1E |
24 |
0E |
5E |
63 |
58 |
D1 |
A2 |
25 |
22 |
7C |
3B |
01 |
21 |
78 |
87 |
| 7 |
D4 |
00 |
46 |
57 |
9F |
D3 |
27 |
52 |
4C |
36 |
02 |
E7 |
A0 |
C4 |
C8 |
9E |
| 8 |
EA |
BF |
8A |
D2 |
40 |
C7 |
38 |
B5 |
A3 |
F7 |
F2 |
CE |
F9 |
61 |
15 |
A1 |
| 9 |
E0 |
AE |
5D |
A4 |
9B |
34 |
1A |
55 |
AD |
93 |
32 |
30 |
F5 |
8C |
B1 |
E3 |
| A |
1D |
F6 |
E2 |
2E |
82 |
66 |
CA |
60 |
C0 |
29 |
23 |
AB |
0D |
53 |
4E |
6F |
| B |
D5 |
DB |
37 |
45 |
DE |
FD |
8E |
2F |
03 |
FF |
6A |
72 |
6D |
6C |
5B |
51 |
| C |
8D |
1B |
AF |
92 |
BB |
DD |
BC |
7F |
11 |
D9 |
5C |
41 |
1F |
10 |
5A |
D8 |
| D |
0A |
C1 |
31 |
88 |
A5 |
CD |
7B |
BD |
2D |
74 |
D0 |
12 |
B8 |
E5 |
B4 |
B0 |
| E |
89 |
69 |
97 |
4A |
0C |
96 |
77 |
7E |
65 |
B9 |
F1 |
09 |
C5 |
6E |
C6 |
84 |
| F |
18 |
F0 |
7D |
EC |
3A |
DC |
4D |
20 |
79 |
EE |
5F |
3E |
D7 |
CB |
39 |
48 |
例如,对于输入 EF, 通过查表输出为 第 E 行,第 F 列,84
继续阅读
SOCKS 是一种网络传输协议,主要用于客户端与外网服务器之间通讯的中间代理传递 。SOCKS是 "SOCKetS" 的缩写。目前其最新的版本是5,相比于前一个版本,其新增了 IPv6, UDP 及 验证。
根据OSI模型,SOCKS是会话层的协议,位于表示层与传输层之间。
协议详情
一个 socks5 连接的过程主要有两部分,协商与请求,如果协商后需要验证,则还包含验证的部分。
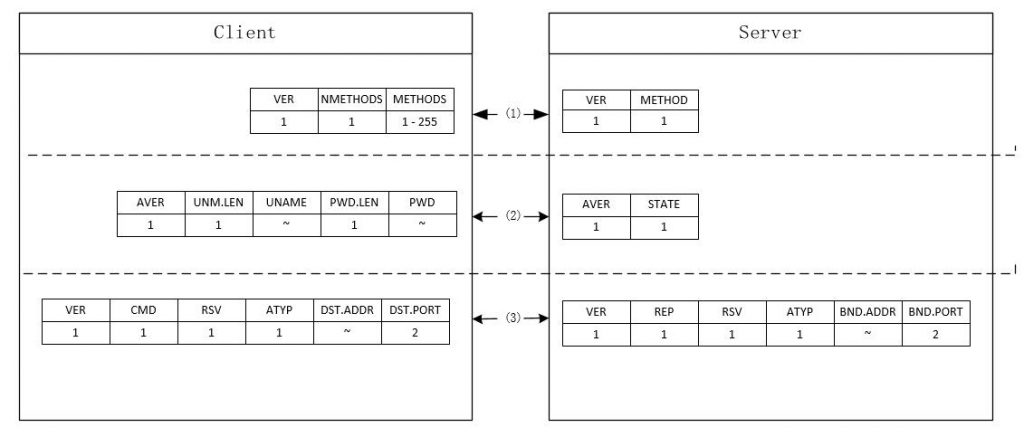
(1) 认证方法协商
客户端向服务端发出连接认证方法协商请求
VER 是 SOCKS 的版本,此处是 0x05NMETHODS 是 METHODS 部分数据的长度,即客户端支持的认证方式的 countMETHODS 是客户端支持的认证方式列表,每个方法占一个字节
0x00 不需要认证0x01 GSSAPI0x02 用户名密码认证0x03 - 0x7F 由 IANA分配(保留)0x80 - 0xFE 私人方法(保留)0xFF 无可接受的方法
服务器回应协商,从客户端提供的方法中选择一个并通知客户端:
VER 是SOCKS的版本号,此处应为 0x05METHOD 是服务端选中的方法。如果不支持客户端提供的所有方法,则返回 0xFF
(2) 认证
继续阅读
 当前的一个项目想使用 Electron 做个 Demo 来进行测试,在调用 C++ 时遇到了一些坑,踩坑的过程中发现网上踩这些坑的人还不少,踩完坑在这里顺手记录一下。
当前的一个项目想使用 Electron 做个 Demo 来进行测试,在调用 C++ 时遇到了一些坑,踩坑的过程中发现网上踩这些坑的人还不少,踩完坑在这里顺手记录一下。
x86 OR x64
lib 的位数与 node.js 的位数必须一致,而和操作系统的位数无关,当然,32位的操作系统是无法运行64位的应用程序 的。
ps: 如何查文件是32位还是64位
- 记得自己下载安装的是什么版本(废话)
- Windows 下:可以使用 vs 自带的 SDK Tools, 执行命令:
继续阅读
一 链表倒置
链表倒置是链表的基本操作之一。
题目 一 Reverse Linked List
LeetCode 206 Reverse Linked List
Reverse a singly linked list.
Example:
Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL
Follow up:
A linked list can be reversed either iteratively or recursively. Could you implement both?
题目提示可以用 迭代 或 递归 两种方法来解。
- 迭代方法
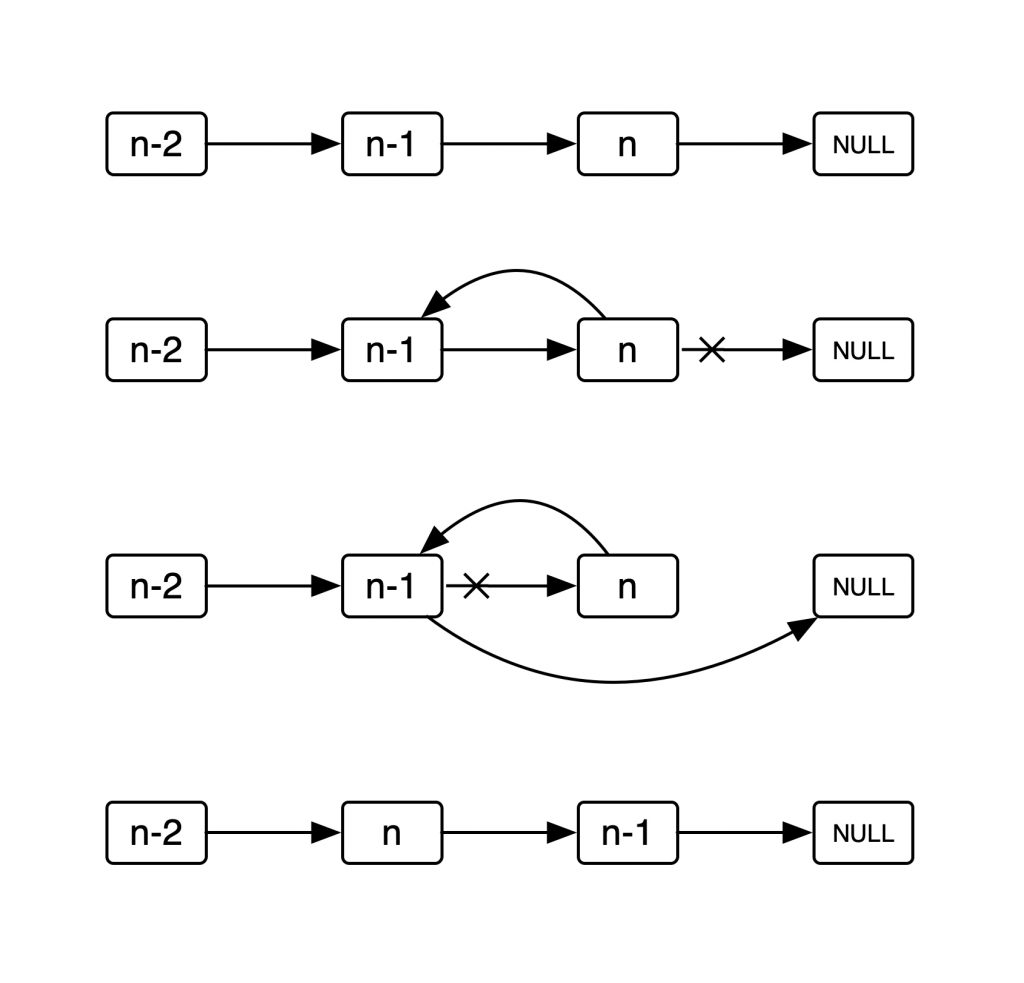
如图:  两个指针
两个指针 head p 分别指向 表头,欲倒置的元素. 为了使下一个欲倒置的元素不会 野 掉, 还需要一个指针 tmp 来保护它
- p->next 指向 head
- head->next 指向 tmp
- head = p, p = tmp, tmp 保护下一个欲倒置的元素
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class Solution { public: ListNode* reverseList(ListNode* head) { if(!head) return NULL; if(!head->next) return head; ListNode *p,*tmp; p = head->next; tmp = p->next; head->next = NULL; while(p1){ p->next = head; head = p; p = tmp; if(tmp) tmp = tmp->next; } return head; } }; |
继续阅读



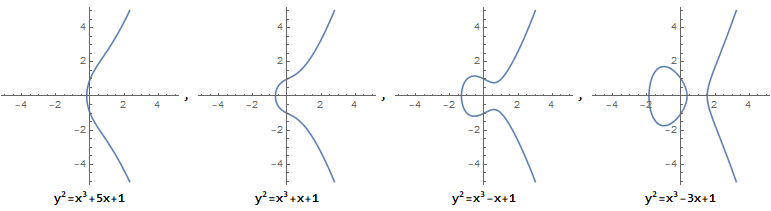
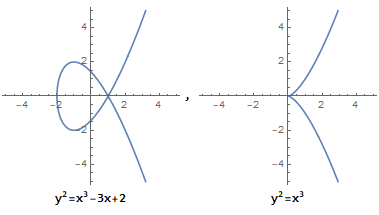

 当前的一个项目想使用 Electron 做个 Demo 来进行测试,在调用 C++ 时遇到了一些坑,踩坑的过程中发现网上踩这些坑的人还不少,踩完坑在这里顺手记录一下。
当前的一个项目想使用 Electron 做个 Demo 来进行测试,在调用 C++ 时遇到了一些坑,踩坑的过程中发现网上踩这些坑的人还不少,踩完坑在这里顺手记录一下。 两个指针
两个指针