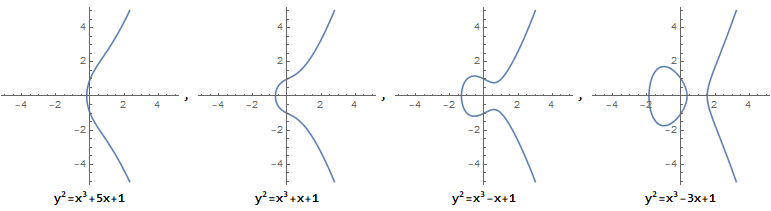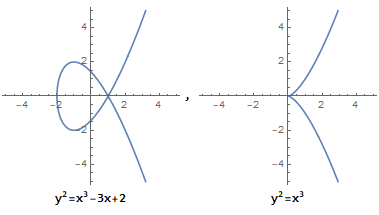没错, 这里说的那个浏览器, 它就是 Chrome 。 以及包括 Edge 在内的绝大多数基于 Chromium 开发的 web浏览器,
我们在登录网站后, 浏览器会提示我们是否保存密钥,我们点下 “是”, 密钥就被浏览器记录。下次打开网站时它甚至会贴心地帮我们自动填充好用户名和密码。我们可以在 chrome://settings/passwords 里查看已保存的密码, 它们会随浏览器账户同步到任何使该浏览器的设备上。当我们要查看某个密码时, 浏览器会要求我们先输入设备密钥。
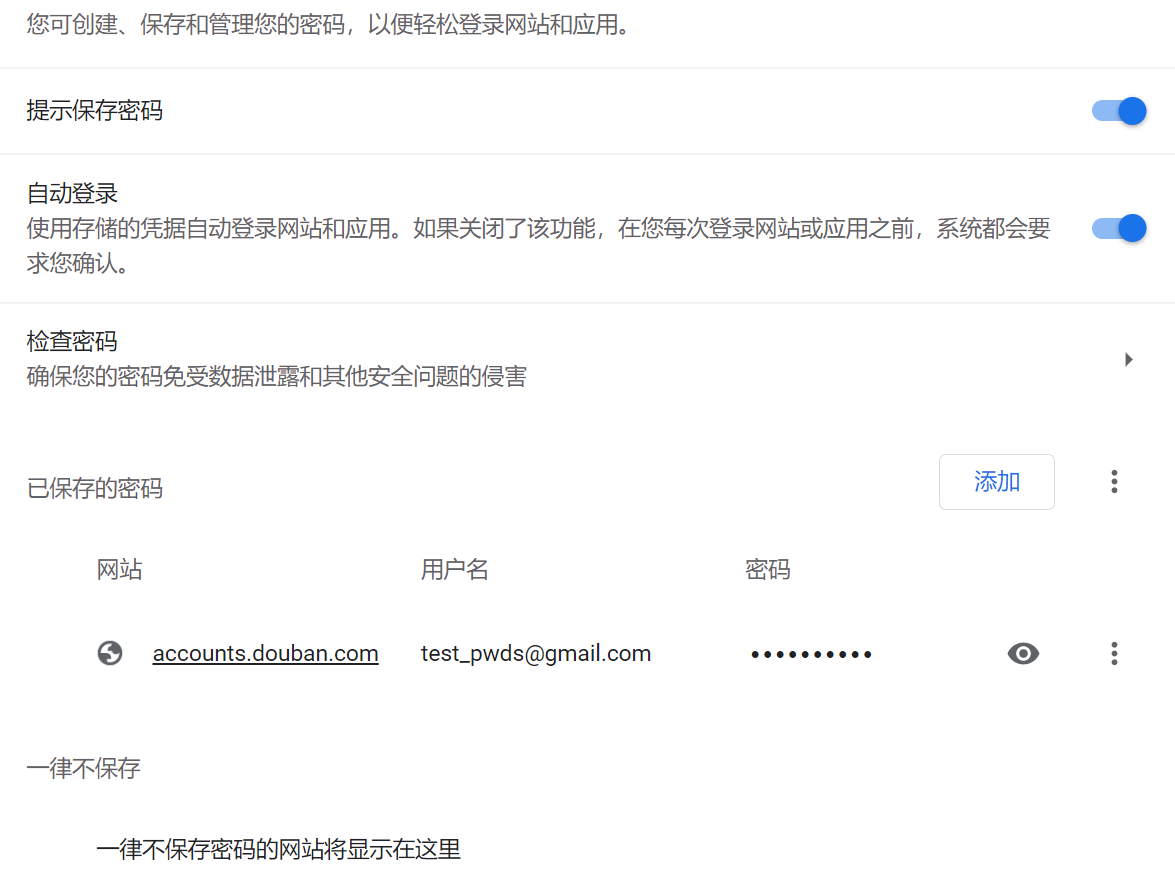
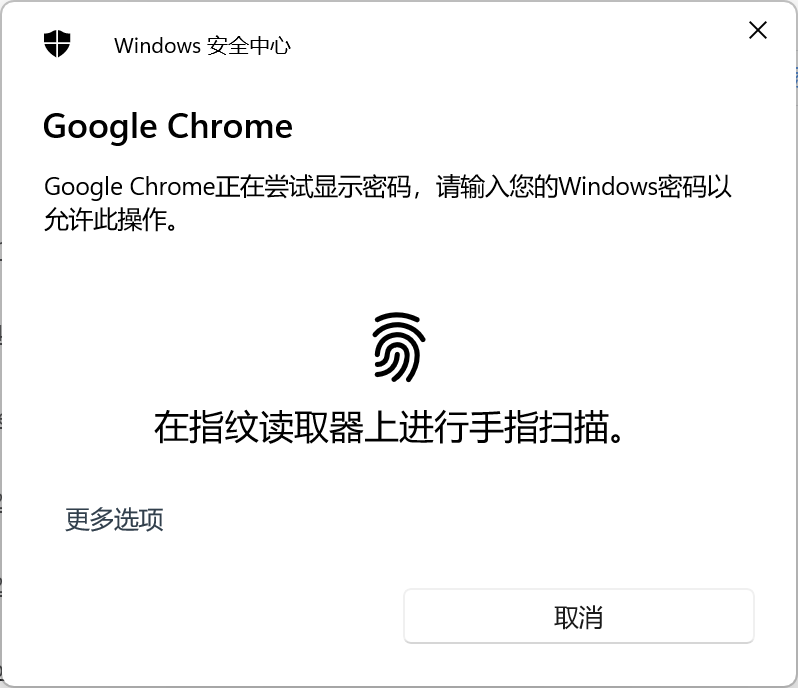
我一直认为它足够安全。直到有一天我研究了 Chromium 的源码。
密码保存的核心代码位于 components\password_manager\core\browser\login_database.cc 。这个文件会对用户输入的密码信息进行保存, 包括网站 URL, 用户名在表单中的元素, 用户名, 密码元素, 密码值等。Chromium 在将密码信息保存在本地时, 对密码值做了加密。但对于其它信息,则完全没有提供任何保密措施。
继续阅读
在之前一篇博客 ECC(Elliptic Curves Cryptography) 椭圆曲线加密原理 简单地阐述了 ECC 加解密的原理。这本篇博客中接着来聊一聊如何使用 OPENSSL 来进行 ECC 加解密。
首先需要明确一点的是:ECC 本身并没有定义一套加解密的方法,它主要作用于密钥交换(ECDHE),与签名认证(ECDSA). 不过后来中国工程师设计定义了一套加密方法,并于近年得到了世界的认可,这就是中国商用(国家标准) SM2 椭圆曲线公钥密码算法 。
一. 基本概念
其实在 openssl 中,椭圆曲线分两种形式,一种是之前讲到的质数域上的椭圆曲线 ,将其称为 $F_p$ 其方程为:
$$y^2 \ \mod \ p = x^3 + ax + b \ \mod \ p$$
另一种是二进制域,称为 $F_{2^m}$, 其方程为:
$$y^2 + xy = x^3 + ax^2 + b ,\ (b != 0)$$
在这里只讨论 $F_p$ 相关的内容。
椭圆曲线上的点
椭圆曲线上的点使用 EC_POINT 来表示, 它定义在 ec_locl.h :
|
|
struct ec_point_st { // ... BIGNUM *X; BIGNUM *Y; BIGNUM *Z; // ... }; |
继续阅读
在我之前的博客中聊到了 DH 密钥交换的原理 . 这里来讨论如何使用 OPENSSL 进行 DH 密钥交换。
一 原理验证
OPENSSL 提供了一系列API, 可以在方便地进行大数计算。在这里我们先对 DH 密钥交换的原理 中讲到的原理进行代码级别的验证。对原理不感兴趣的可以跳过这一小节。
由于在 DH 密钥交换过程中,大部分的操作过程都是一样的,可以定义一个基类来抽象:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
class DHBase { public: DHBase() : m_pri_key(NULL) {} virtual ~DHBase() { if (m_pri_key) BN_free(m_pri_key); }; const BIGNUM *GetSharedNum() { if (!m_pri_key) GenRandomData(); BN_CTX *ctx = BN_CTX_new(); const BIGNUM *g = DH_get0_g(m_dh); const BIGNUM *p = DH_get0_p(m_dh); BIGNUM *r = BN_new(); // r = g ^ m_pri_key % p int rst = BN_mod_exp(r, g, m_pri_key, p, ctx); assert(rst == 1); BN_CTX_free(ctx); return r; } BIGNUM *GenKey(const BIGNUM *shared_num) { if (!m_pri_key) GenRandomData(); BIGNUM *key = BN_new(); BN_CTX *ctx = BN_CTX_new(); // key = shared_num ^ m_pri_key % p int rst = BN_mod_exp(key, shared_num, m_pri_key, DH_get0_p(m_dh), ctx); assert(rst == 1); BN_CTX_free(ctx); std::cout << m_name << ": received shared num: " << GetNumString(shared_num) << std::endl; std::cout << m_name << ": generated KEY: " << GetNumString(key) << std::endl; return key; } std::string GetName() { return m_name; } static std::string GetNumString(const BIGNUM *num) { return BN_bn2hex(num); } private: void GenRandomData() { assert(m_dh); m_pri_key = BN_new(); int rst = BN_rand_range(m_pri_key, DH_get0_p(m_dh)); assert(rst == 1); while (BN_is_zero(m_pri_key)) { BN_rand_range(m_pri_key, DH_get0_p(m_dh)); } std::cout << m_name << ": generated the private num" << std::endl; } protected: DH *m_dh; std::string m_name; private: BIGNUM *m_pri_key; }; |
m_pri_key 是双方生成的私密随机数。GetSharedNum() 返回双方交换的中间变量 G^A mod PGenKey() 即完成了密钥交换,返回交换成功后的密钥。
继续阅读
在我之前的一篇博客中 RSA 公钥加密原理 中, 对 RSA 非对称加密原理做了简单的阐述。这篇博客主要聊如何使用 OPENSSL 进行密钥对的生成,以及非对称加解密。
一. 生成密钥对
在 OPENSSL 中, RSA 是一个很重要的结构体。它的定义在 rsa_locl.h 中,面包含了在原理中提到的所有重要的变量 随机质数 p, q, 公钥指数 e, 私钥指数 d, 以及模数 n
|
|
struct rsa_st { // ... BIGNUM *n; BIGNUM *e; BIGNUM *d; BIGNUM *p; BIGNUM *q; // ... }; |
生成密钥函数:
|
|
int RSA_generate_key_ex(RSA *rsa, int bits, BIGNUM *e, BN_GENCB *cb); |
bits 密钥的规模(modulus)。小于 1028 位的密钥是不安全的,小于 512 则会返回 0e 公开的指数。它应该是一个奇数(odd number), 一般是 3, 17 或 65537cb 生成大随机数的回调函数。一般使用 NULL 即可, 默认为 BN_GENCB_call()
继续阅读
在我之前的一篇博客里介绍了 对称加密的模式 .  这里主要聊一聊如何使用
这里主要聊一聊如何使用 openssl 来进行 AES 加密 .
一. OPENSSL crypto API
openssl 加密 API 分两个部分: High Level and Low Level . 对于大部分人来说,使用 High Level 就够用了, 这些 API 被冠以 EVP (Envelope) ,表示对 Low Level 的封装。High Level API 提供了包括 对称/非对称加解密 , 签名, 验证, 哈希,MAC 等一系列组件,屏蔽了 Low Level API 的复杂逻辑,使用起来安全高效。对于除非有需要进行加密算法级别的改进,否则不建议使用 Low Level API.
大部分 EVP API 有一个 int 型返回值 ,用来表示操作是否成功:1 表示成功, 0 表示失败。但有些时候也会返回 -1 ,表达如内存分配或者其他什么错误。官方指导代码如下:
|
|
if(1 != EVP_xxx()) goto err; if(1 != EVP_yyy()) goto err; /* ... do some stuff ... */ err: ERR_print_errors_fp(stderr); |
二. 使用 EVP API 进行 AES 加解密
对于 AES 加解密,EVP API 分为两种,EVP_Encrypt / EVP_Decryp 系列 和 EVP_Cipher 系列。后者是对前者进一步的封装。它们具体使用的套路都是一样的:
- 创建加解密上下文
EVP_CIPHER_CTX
- 调用
xxxInit() 函数,使用 key(密钥)、iv(前置向量) 和 cipher(算法) 对上下文初始化
- 调用
xxxUpdate() 函数进行加解密。该函数支持流式操作。即对于一段明文来说,分成多组按顺序进行加密,和一次性全部加密,不影响其生成的密文的正确性。
- 调用
xxxFinal() 函数获取上下文中遗留的信息
- 释放上下文, 完成加解密。
继续阅读
和对称加密不同,公钥加密(非对称加密)的密钥分为加密密钥(公钥)和解密密钥(私钥)。 公钥是公开的,任何人都有可能知道公钥,并用公钥生成密文,而私钥是保密的,只有解密者才能知道私钥,用它来解密密文获得明文。在这里对使用最广泛的公钥密码算法-- RSA.
RSA 是发明此算法的三位科学家的姓氏的首字母(吐槽一下:外国人的命名真随意)
一. RSA 加密
在RSA中,明文,密钥和密文都是数字, RSA的加密过程可以用如下公式表达:
$$密文 = 明文^E \mod N$$
即: RSA 的密文是明文的 $E$ 次方求模 $N$ 的结果, 或者说,密文是明文的 $E$ 次方除以 $N$ 的余数。这就是整个加密过程,它非常简洁。因此,如果知道了 $E$ 和 $N$ ,那么任何人都可以进行加密运算,也就是说,
$$ E 和 N 是公钥$$
在实际使用中, E 和 N 是经精心计算的数字。
二. RSA 解密
RSA 解密公式如下:
$$ 明文= 密文^D \mod N$$
即,对密文的 $D$ 次方求模 $N$ 运算,就可以得到明文。这里是
$$D 和 N 是私钥 $$
继续阅读
在使用对称加密中,有一些无法避免的问题:
- 密钥如何从加密方传递给解密方。窃听者如果可以劫获密文,那么也可能劫获密钥。
- 如果窃听者破解了密钥,加密方如何将新的密钥安全地交给解密方
1. DH 密钥交换
解决上述问题的一种方法就是 DH 密钥交换 技术 。
DH 密钥交换全称为 Diffie-Hellman 密钥交换 ,是1976年由 Whitfiedl Diffle 和 Martin Hellman 共同发明的一种算法。使用这种方法,通信双方可以在窃听者眼皮子底下来安全地传输密码。
DH 交换的步骤如下:
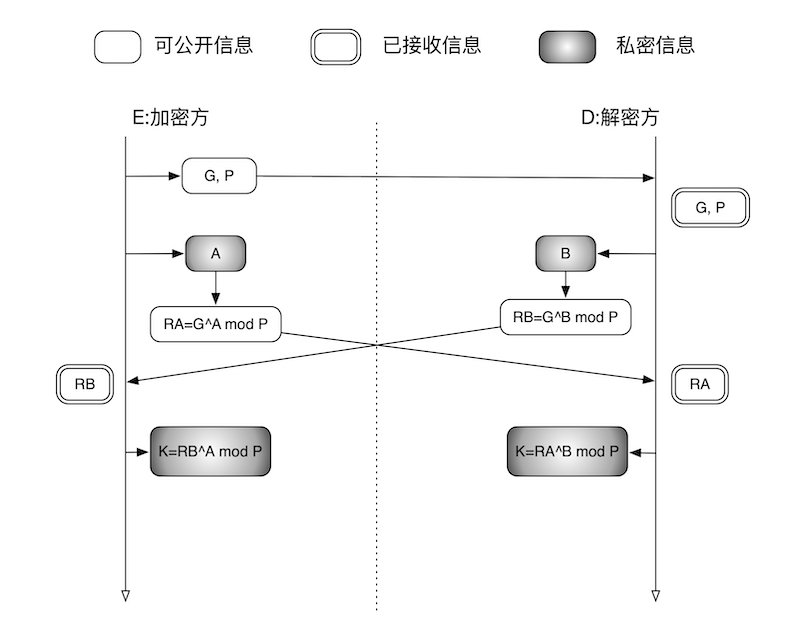
继续阅读
ECC(Elliptic Curves Cryptography) 属于非对称加密算法的一个重要组成部分。
本文尽量简单地阐述椭圆曲线加密的原理,但需要读者有一些初级的数论与离散数学相关的知识,或者推荐简单地阅读《算法导论》第31章:数论算法。
椭圆曲线
首先需要明确的是,我们讨论的是什么样的曲线。
椭圆曲线有比较复杂的定义: https://en.wikipedia.org/wiki/Elliptic_curve .而我们讨论的椭圆曲线比这个简单,它是以下方程所描述的一条平滑曲线 :
$$y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0$$
它描述的并不是一个椭圆,之所以称它为"椭圆曲线方程", 是因为它源自于求椭圆弧长的椭圆积分的反函数。椭圆曲线是无奇点的,即没有尖点,且不会自相交。当 $a,b$ 的值不同时,椭圆曲线会表现出不同的形态:
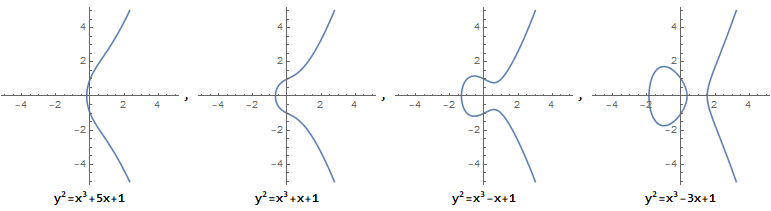
而当 $4a^3 + 27b^2 = 0$ 时, 它不是椭圆曲线:
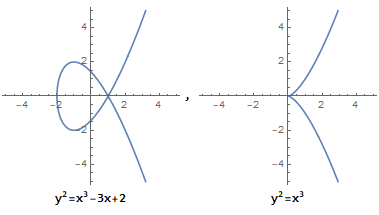
从图中可以看到,椭圆曲线总是 沿 x 轴对称 的。这是因为 $y^2$ 的存在。特殊地,我们规定 无穷远点 也存在于椭圆曲线上。我们用 $0$ 或符号 $O$ 来表示无穷远点,则椭圆曲线在实数域上的定义如下:
$$\{ (x,y) \in \mathbb{R}^2 | y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}$$
继续阅读


 这里主要聊一聊如何使用
这里主要聊一聊如何使用