例题 一 : Triangle
LeetCode 120. Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
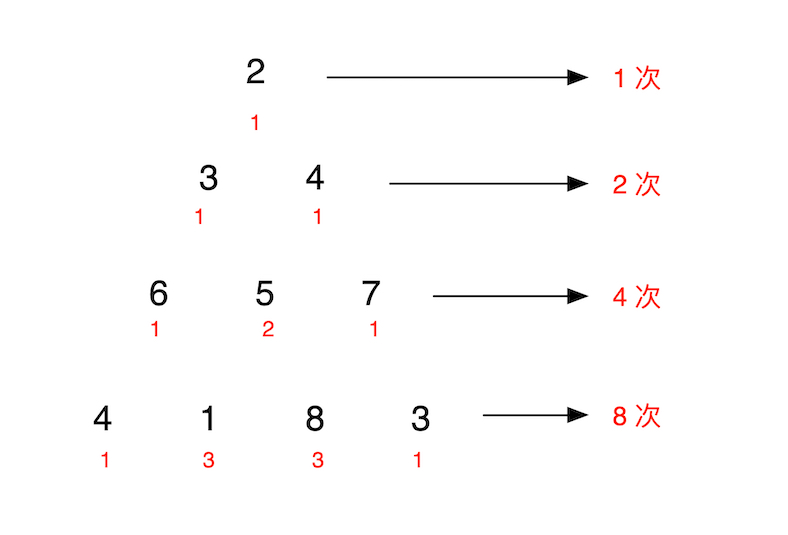
For example, given the following triangle[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
分析:
设三角形共有 $N$ 行, $r$ 为三角形的行, $c$ 为三角形的列。从点 $P(r,c)$ 出发,每向下走一步有两个点$P_1(r+1,c), P_2(r+1, c+1)$ 可以选择 ,如果每次都选值小的点$min(P1, P2)$,则最后得到的点的值之和即是最优解。令 $M(r,c)$ 为从 $P(r,c)$ 开始到下面的列的各条路径中,最佳路径的数字之和。
解法一:
这是一个典型的递归问题。
$$M(r,c) = \begin{cases} P(r,c), & \text{if r = N }\\ min(M(r+1,c), M(r+1,c+1)) + P(r,c),& \text{others}\\ \end{cases}$$
由此写出代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class Solution { public: int getMinPathSum(vector<vector<int>>& triangle, int r, int c){ if(r == triangle.size() - 1) return triangle[r][c]; int x = getMinPathSum(triangle, r+1, c); int y = getMinPathSum(triangle, r+1, c+1); x = x<y ? x: y; return triangle[r][c] + x; } int minimumTotal(vector<vector<int>>& triangle) { return getMinPathSum(triangle, 0,0); } }; |
代码没有问题,在 "Run Code" 时可以得出正确的结果。但是 "Submit" 却会给出 "Time Limit Exceeded",超时!
如果我们推算这个解法的时间复杂度的话,可以得到 $O(2^n)$ .这不超时就有鬼了。我们需要改进这个算法。