算法学习:动态规划问题的一般解法
目录
例题 一 : Triangle
LeetCode 120. Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
分析:
设三角形共有 $N$ 行, $r$ 为三角形的行, $c$ 为三角形的列。从点 $P(r,c)$ 出发,每向下走一步有两个点$P_1(r+1,c), P_2(r+1, c+1)$ 可以选择 ,如果每次都选值小的点$min(P1, P2)$,则最后得到的点的值之和即是最优解。令 $M(r,c)$ 为从 $P(r,c)$ 开始到下面的列的各条路径中,最佳路径的数字之和。
解法一:
这是一个典型的递归问题。
$$M(r,c) = \begin{cases} P(r,c), & \text{if r = N }\\ min(M(r+1,c), M(r+1,c+1)) + P(r,c),& \text{others}\\ \end{cases}$$
由此写出代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class Solution { public: int getMinPathSum(vector<vector<int>>& triangle, int r, int c){ if(r == triangle.size() - 1) return triangle[r][c]; int x = getMinPathSum(triangle, r+1, c); int y = getMinPathSum(triangle, r+1, c+1); x = x<y ? x: y; return triangle[r][c] + x; } int minimumTotal(vector<vector<int>>& triangle) { return getMinPathSum(triangle, 0,0); } }; |
代码没有问题,在 "Run Code" 时可以得出正确的结果。但是 "Submit" 却会给出 "Time Limit Exceeded",超时!
如果我们推算这个解法的时间复杂度的话,可以得到 $O(2^n)$ .这不超时就有鬼了。我们需要改进这个算法。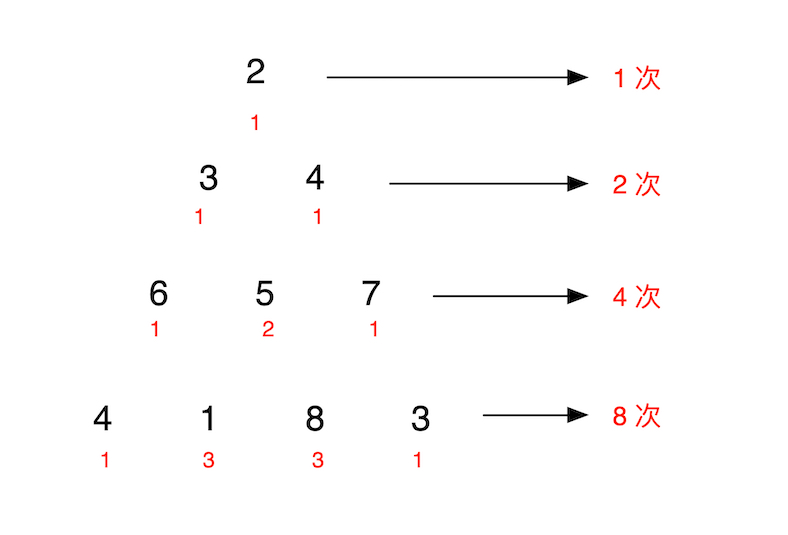
解法二:
可以看出,$M$ (即getMinPathSum) 被重复计算了,越是靠近三角形底部、越是靠近每行的中心,重复计算的次数越多。设想:假如当我们第一次算出 $M(r,c)$ 时, 就将其保存到某个地方 $T(r,c)$,下次需要计算 $M(r,c)$的时候直接取 $T(r,c)$,那不就可以避免重复计算了吗,这样时间复杂度可以降到 $O(n^2)$ , 因为该三角形中的数字的总个数为 $\frac {n(n+1)}{2}$ 。如下代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Solution { public: struct MinVal{ bool flag; //是否已设置了值 int val; MinVal():flag(false),val(0){}; }; int getMinPathSum(vector<vector<int>>& triangle, int r, int c, vector<vector<MinVal>>& tmp){ if(r == triangle.size() - 1) return triangle[r][c]; //最后一行不用保存 if(tmp[r][c].flag) return tmp[r][c].val; int x = getMinPathSum(triangle, r+1, c, tmp); int y = getMinPathSum(triangle, r+1, c+1, tmp); x = x<y ? x: y; //算过的值,保存起来 x = triangle[r][c] + x; tmp[r][c].val = x; tmp[r][c].flag = true; return x; } int minimumTotal(vector<vector<int>>& triangle) { //构造临时空间 vector<vector<MinVal>> tmp(triangle.size()); for(int i = 0; i<tmp.size(); ++i){ tmp[i] = vector<MinVal>(triangle[i].size()); } return getMinPathSum(triangle, 0,0, tmp); } }; |
一个小结:
在解题的过程中,我们思路:
- 将一个求最优解的问题分解成求多个最优解的子问题 (定义 $M(r,c)$ 的过程 )
- 意识到子问题会重复计算
- 将会被重复计算的子问题的解存储起来。且不会改变。
这种求解具有 重叠子问题 的 最优解 的问题的过程中,避免子问题被重复计算而将子问题的解 存储 起来的算法,可以称之为 动态规划 算法。我们可把子问题叫做 状态 ,在方法二中,从求子问题的解到将子问题的解存储起来的过程,看做是从一种状态到另一状态的 转移 。
再将上面的思路总结一下,即为动态规划算法的适用性:
- 最优子结构性质:问题的最优解所包含了子问题的解也是最优的;
- 子问题重叠性质:每次产生的子问题并不总是新问题。动态规划利用该性质将每个子问题的解存储,该子问题不再进行重复计算;
- 状态转移无后效性质: 子问题的解一旦确定,将不会再改变。
解法三:
上面的解法是自顶而下的递归解法。根据以上三个性质,我们也可以尝试自下而上的来解问题。即从最后一行开始,算出每个点的最优解,一直算到顶点,该顶点的解即是最优解:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
class Solution { public: int minimumTotal(vector<vector<int>>& triangle) { if(triangle.size() == 1) return triangle[0][0]; //构造临时空间 vector<vector<int>> tmp(triangle.size()); for(int r = 0; r<tmp.size(); ++r){ tmp[r] = vector<int>(triangle[r].size()); } for(int r = triangle.size()-1; r >= 0 ; --r){ for(int c = 0; c < triangle[r].size(); ++c){ if(r == triangle.size() - 1){ tmp[r][c] = triangle[r][c]; } else{ tmp[r][c] = triangle[r][c] + (tmp[r+1][c] < tmp[r+1][c+1] ?tmp[r+1][c] : tmp[r+1][c+1] ); } } } return tmp[0][0]; } }; |
这种思路将递归的解法改造成递推的解法,更容易理解。
解法四:
解法二、三都构造了一个与三角形等大的数组。空间复杂度大大增加了($O(r^2)$)。可不可以改进呢?可以的,实际上,在递推的过程中,当 $T(r+1)$ 被 $M(r)$ 使用以后不会再参与计算,可以使用 $T(r)$ 覆盖 $T(r+1)$,这样临时空间只需要大小的 $r$ 即能完全够用。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class Solution { public: int minimumTotal(vector<vector<int>>& triangle) { if(triangle.size() == 1) return triangle[0][0]; //构造临时空间 vector<int> tmp(triangle[triangle.size()-1].size()); for(int r = triangle.size()-1; r >= 0 ; --r){ for(int c = 0; c < triangle[r].size(); ++c){ if(r == triangle.size() - 1){ tmp[c] = triangle[r][c]; } else{ tmp[c] = triangle[r][c] + (tmp[c] < tmp[c+1] ? tmp[c] : tmp[c+1] ); } } } return tmp[0]; } }; |
同理,可以再优化:当完成 $M(r,c)$ 后,$P(r, c)$ 将不再参与计算,这个空间是可以拿来利用的,可以用其来存储 $M(r,c)$ 。这样最终结果存储在 $P(0,0)$ 中。即在上面代码中,最后返回的结果是 triangle[0][0] . 代码略。
例题 二:Maximum Subarray
LeetCode 53. Maximum Subarray
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
解法一:
朴素的递归方法。
分析:求和最大的子数组。设 $S_i$ 为从 $i$ 开始的, 有最大和的子数组之和, 那么该问题的解即为求 $S_0, S_1, \dots , S_n$ 中的最大值。
$$ S_i = \begin{cases} nums[i], & \text{if } i ==n ;\\max(nums[i], nums[i] + S_{i+1}), & \text{Others} \\ \end{cases}$$
相应的代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
class Solution { public: int getMaxSum(vector<int>& nums, int i){ if(i == nums.size() - 1) return nums[nums.size()-1]; return std::max(nums[i] + getMaxSum(nums, i+1),nums[i]); } int maxSubArray(vector<int>& nums) { if(nums.size() == 1) return nums[0]; vector<int> maxs(nums.size()); for(int i = 0; i<nums.size(); ++i){ maxs[i] = getMaxSum(nums,i); } return *std::max_element(maxs.begin(), maxs.end()); } }; |
解法二:
动态规划法:
状态转移: 将以第 $i$ 个元素开头的子数组的最大和存储在临时变量中,使其不用在下次使用时再计算一遍。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
class Solution { public: struct Val{ bool flag; int val; Val():flag(false), val(0){}; }; int getMaxSum(vector<int>& nums, int i, vector<Val>& tmp){ if(i == nums.size() - 1) return nums[nums.size()-1]; if(tmp[i].flag) return tmp[i].val; tmp[i].val = std::max(nums[i] + getMaxSum(nums, i+1, tmp),nums[i]); tmp[i].flag = true; return tmp[i].val; } int maxSubArray(vector<int>& nums) { if(nums.size() == 1) return nums[0]; vector<Val> maxs(nums.size()); for(int i = 0; i<nums.size(); ++i){ nums[i] = getMaxSum(nums,i, maxs); } return *std::max_element(nums.begin(), nums.end()); } }; |
解法三:
动态规划递推:
思路转变:从后往前,依次求出以元素 nums[i] 的最优解(即以nums[i] 起始的子数组的最大和 tmp , 此值将参与求元素 nums[i-1] 最优解的运算一次。解法如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
class Solution { public: int maxSubArray(vector<int>& nums) { if(nums.size() == 1) return nums[0]; int tmp, maxVal; tmp = maxVal = nums[nums.size()-1]; for(int i = nums.size()-2; i>=0; --i){ tmp = std::max(nums[i], nums[i] + tmp); maxVal = std::max(maxVal, tmp); } return maxVal; } }; |
这样该题的时间复杂度为 $O(n)$ . 当然该题的题目里也提示了,可以尝试使用分治法解决该问题,下次再讨论。
LeetCode 上的其他类似题目:
- 53 Jump Game
- 152 Maximum Product Subarray
- 98 House Robber
- 待补充
注意152 Maximum Product Subarray与98 House Robber子问题产生了变种,状态可能会改变,但这种改变是可控的。
再一个小结:
对于:可以分解成多个重复的子问题、求最优解 的题目,可以尝试使用动态规划的方法来解题。解决了局部的最优解, 即能得到全局的最优解。如果题目比较简单,可以尝试使用直接递推法,否则可以先进行子问题的分解,使用递归的方法解题,再对递归内的状态进行转移,优化成动态规划的解法。