Mathematica 的几个技巧
目录
绘图
画曲线的交点
有多种方法。
一是利用
Mesh ,MeshFunction, 二是求出点,并使用 Graphicseg.1:
|
1 2 3 4 5 6 |
(*Mesh*) Plot[{Sin[x], 1/x},{x,0,6Pi},Mesh->{{0}}, MeshFunctions->Function[x,1/x-Sin[x]], MeshStyle->Directive[PointSize[.02], Red]] (*Graphics*) pts = NSolve[Sin[x] == 1/x && 0<x<6Pi && y == 1/x,{x,y}]; Show[Plot[{Sin[x], 1/x},{x,0,6Pi}], Graphics[{Red,PointSize[0.02],Point[{x,y} /. pts]}]] |

eg.2:
|
1 2 3 4 5 6 |
(*Mesh*) ContourPlot[{y^2 == x^3 + 3, x^2 + y^2 == 4},{x,-5,5},{y,-5,5}, Axes->True, Mesh->{{0}}, MeshStyle->Directive[PointSize[.02], Red], MeshFunctions->Function[x, 4-x^2 - (x^3 + 3)]] (*Graphics*) pts = NSolve[y^2 == x^3 + 3 && x^2 + y^2 == 4 && -5 < 0 < 5 && -5 <y < 5,{x,y}]; Show[ContourPlot[{y^2 == x^3 + 3, x^2 + y^2 == 4},{x,-5,5},{y,-5,5},Axes->True], Graphics[{Red,PointSize[0.02],Point[{x,y}/.pts]}]] |

文本偏移与旋转
文本绘制使用 Text[expr,coords,offset,dir] ,其中 offset 为偏移量,单位为一个 point(一般是 1/72 inc) 。 dir 为文本的方向
eg.1 偏移
|
1 2 |
Pt = {3,3}; Show[ {Graphics[{ Text[A,Pt,{2,2}], Text[B, Pt,{2,-2}], Text[C,Pt,{-2,2}], Text[D,Pt,{-2,-2}]}], Graphics[{Red, PointSize[.02], Point[Pt]}]}, Axes->True] |

|
1 2 3 4 5 6 7 8 9 |
Graphics[{ Text["ABC 1->0", {0, 0}, {0, 0}, {1, 0}],(* 正常 *) Text["ABC 1->1", {1, 0}, {0, 0}, {1, 1}], (* 45 *) Text["ABC 0->1", {2, 0}, {0, 0}, {0, 1}], (* 90 *) Text["ABC -1->1", {3, 0}, {0, 0}, {-1, 1}], (* 135 *) Text["ABC -1->0", {4, 0}, {0, 0}, {-1, 0}], (* 180 *) Text["ABC 1->-1", {5, 0}, {0, 0}, {1, -1}], (* 225 *) Text["ABC 0->-1", {6, 0}, {0, 0}, {0, -1}] (* 270 *) }, Axes -> False] |
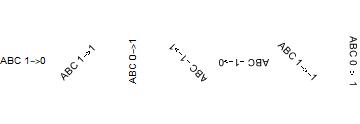
计算
求模等方程
|
1 2 |
pts =Solve[Reduce[Mod[y^2, 23] == Mod[x^3 + x + 1, 23], {x,y},Integers] && 0<= x < 23 && 0<= y < 23]; {x,y} /. pts |
|
1 2 3 |
output = {{0, 1}, {0, 22}, {1, 7}, {1, 16}, {3, 10}, {3, 13}, {4, 0}, {5, 4}, {5, 19}, {6, 4}, {6, 19}, {7, 11}, {7, 12}, {9, 7}, {9, 16}, {11, 3}, {11, 20}, {12, 4}, {12, 19}, {13, 7}, {13, 16}, {17, 3}, {17, 20}, {18, 3}, {18, 20}, {19, 5}, {19, 18}} |